Min første runde 2-oppgave
Fra runde 1 til runde 2 i Nio endres formatet på oppgavene, som du kan lese om på siden om rundene. Hovedforskjellen er at runde 1 kan løses med kun mus, og du får se oppgaven visuelt. I runde 2 er oppgaver gitt som tekst, og besvarelsen skal være et program som oppfører seg som beskrevet i oppgaveteksten, som du må programmere selv. Når du leverer inn et forsøk, testes programmet ditt på et sett med hemmelige tester, og du får bare poeng hvis programmet ditt gir eksakt riktig svar på testene, uten å krasje eller bruke for lang tid.
Dette formatet kan fort virke skremmende, men å kunne skrive effektiv og korrekt kode gitt en presis oppgavebeskrivelse er en svært verdifull ferdighet, og det er dette formatet som brukes i internasjonale informatikk-konkurranser.
Teksteditor
For å komme i gang må du ha en teksteditor for å skrive kode på maskinen din. Runde 2 utføres på egen maskin, så du kan fritt installere den editoren du vil. Visual Studio Code er et populært valg, som støtter alle tillatte programmeringsspråk i Nio. Et enklere alternativ som kommer inkludert med Python-installasjoner er IDLE, som gir deg akkurat nok funksjonalitet til å skrive besvarelser i Python, og teste Python-koden. I denne gjennomgangen bruker vi IDLE.
Eksempeloppgave
På resten av denne siden skal vi ta for oss følgende oppgave fra runde 2, 2019/2020:

Oppgaveteksten beskriver oppgaven som programmet ditt skal kunne løse: “Gitt en liste med positive heltall, finn det laveste tallet som kun forekommer én gang i listen”. Besvarelsen din skal være et program som løser dette problemet for en hvilken som helst liste. Du får oppgitt en presis beskrivelse av formatet til input som programmet må lese inn, og en beskrivelse av output som programmet må printe ut når det har funnet svaret. Lenger ned i oppgaveteksten vil du se eksempler på tester programmet ditt skal evalueres på:

Dette forteller oss at en korrekt løsning på oppgaven vil være et program som svarer 8 gitt listen i eksempel 1, og -1 gitt listen i eksempel 2. Merk at det første tallet i input ikke er en del av listen, men er lengden på den påfølgende listen med tall.
Lese inn input
La oss nå skrive et program som løser oppgaven.
Til å begynne med bruker vi Python, og IDLE-editoren.
Første steg er dermed å åpne IDLE, og lage en ny fil, som kan hete hva som helst, f.eks. uniketall.py.
Her skriver vi
# Hvor lang listen skal være
N = int(input())
# Begynn med en tom liste, og legg til N tall
liste = []
for i in range(N):
tall = int(input())
liste.append(tall)
Hvert kall til input() leser en ny linje fra input.
Siden det som leses inn er tekststrenger, må vi pakke kallet inn i int() for å gjøre det om til tall.
Det er også viktig at vi ikke skriver noe slik som input("Hvor lang er listen?"), siden det vil printe Hvor lang er listen?
til konsollen. Output skal kun inneholde ett tall, som beskrevet i oppgaveteksten, og da kan vi ikke printe noen andre ting.
for-løkken brukes for å kalle input() N ganger til, slik at hele listen blir lest inn.
For flere tips til lesing av input, se Hvordan lese input.
Algoritmen
Nå som input er lest inn, og ligger i listen liste, kan vi forsøke å løse oppgaven.
Vi blir bedt om å finne det laveste unike tallet, så en god start kan være å finne alle unike tall.
Denne nye listen kaller vi unike_tall. For å fylle listen kan vi for eksempel gå gjennom hvert tall i liste,
og bruke liste.count(tall) for å sjekke hvor mange ganger tall forekommer. Hvis tall kun forekommer 1 gang, er det et unikt tall.
# Alle tall som forekommer nøyaktig én gang i liste
unike_tall = []
for tall in liste:
if liste.count(tall) == 1:
unike_tall.append(tall)
Printe output
Nå som vi har en liste med unike tall, kan vi bruke min()-funksjonen for å finne det laveste unike tallet.
Det eneste vi må huske på er at det potensielt ikke er noen unike tall, slik som i eksempel 2. Da vil unike_tall være en tom liste,
og vi skal printe -1 i stedet.
# Print laveste unike tall, eller -1 om ingen tall er unike
if len(unike_tall) == 0:
print(-1)
else:
print(min(unike_tall))
Teste programmet
Nå kan vi teste programmet vårt. I IDLE bruker du Run -> Run Module for å kjøre programmet,
som vil starte i IDLE-shell-vinduet.
Det kan virke som at ingenting skjer, men det er fordi programmet venter på input.
Begynn med å skrive inn en av eksempel-inputene, og trykk enter mellom hver linje.
Når den siste linjen er skrevet inn, vil algoritmen kjøre, og ganske fort printe ut svaret i blå tekst.
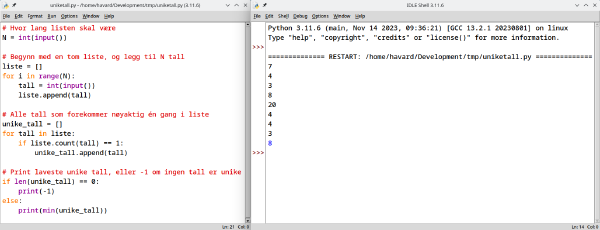
Dersom du prøver inputen fra eksempel 2, vil du se at du får -1 som svar, slik som forventet.
Du kan også lage dine egne lister å teste på, bare husk at det førse tallet du skriver inn ikke er en del av listen, men lengden på den påfølgende listen.
Levere programmet på konkurranseserveren
Hadde dette vært en ordentlig konkurranse hadde du allerede vært logget inn på en konkurranseserver på dette punktet,
men dette er bare trening. Derfor kan vi lage oss en bruker på trenings-serveren, som inneholder gamle oppgave fra både runde 2 og finalen.
På toppen av siden finner du Registrer ny bruker. Etter du har laget en bruker logger du inn på Trenings-system.
Langs venstresiden av skjermen finner du oppgavene på serveren, og i blant dem ligger oppgaven vi har jobbet med, nio20-runde2-talllek.
Ved å trykke på Statement får du mulighet til å laste ned oppgaveteksten, mens Submissions tar deg til innlevering av besvarelser.
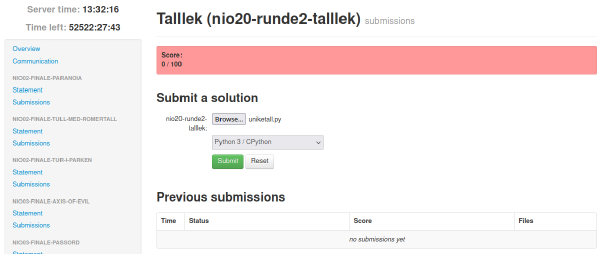
nio20-runde2-talllek. Her kan du trykke Browse, velge filen du lagret besvarelsen din i, passe på at språket er valgt som Python 3, og trykke Submit. Etter litt ventetid vil du se hvor mange poeng du fikk. I vårt tilfelle fikk vi 55 / 100 poeng.

nio20-runde2-talllek. Ved å trykke details får vi opp detaljer som forklarer hvorfor vi ikke fikk 100 poeng.
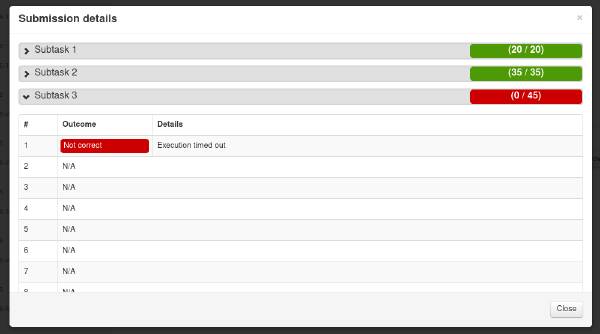
nio20-runde2-talllek.
Her ser vi at vi fikk poeng på subtask 1 og subtask 2,
mens subtask 3 fikk feilkoden Execution timed out på aller første test.
Når en test i en subtask feiler, får vi ikke noe poeng for den subtasken, og serveren hopper over å kjøre noen flere tester i den subtasken.
I dette tilfellet brukte programmet for lang tid på en test som tilhørte subtask 3.
Subtasks / testsett
I oppgaveteksten står det oppgitt en liste med begrensninger, som gir visse garantier om hva slags input programmet kan bli testet på. I tillegg er testene inndelt i grupper, der noen av gruppene har strengere begrensninger på testenes input. Dersom programmet ditt klarer alle testene i en gruppe, får den poeng for den gruppa, uavhengig av hvordan programmet gjør det på testene i de andre gruppene. Grupper med strengere begrensninger vil generelt være lettere å løse, siden programmet får flere garantier om hvordan input ser ut. Selv om en oppgave totalt sett er for vanskelig, kan du skrive programmer som kun fungerer på noen av testgruppene, og likevel få noen poeng. Derfor kalles testgrupper også for subtasks.

I vårt tilfelle fikk vi poeng på subtask 1 og 2, og fikk dermed til alle testene der N var mindre enn eller lik 5000.
Så snart N kunne være større enn 5000, helt opp til 50 000 (som beskrevet i de generelle begrensningene), oppsto problemer.
Execution timed out betyr at programmet brukte mer enn den definerte tidsbegrensningen på 1 sekund, når N ble større.
Kjøretidsanalyse
La oss studere hvordan kjøretiden til programmet påvirkes av lengden på listen N.
Tiden brukt på å lese inn tall vokser lineært med størrelsen på listen. Er listen dobbelt så lang, forventer vi at det tar omtrent dobbelt så lang tid å lese inn alle tallene. Med en liste på maks 50 000 elementer, burde dette være en smal sak for datamaskinen, så det er ikke her programmet blir tregt.
Neste steg er å finne unike elementer. Her bruker vi count(tall), og vi vet at vi kaller funksjonen N ganger.
Hver gang vi kaller count(tall), blir hvert element i listen sammenlignet med tall.
Siden listen er N elementer lang, foretas det N sammenligninger for hvert kall av count(tall).
Totalt blir det dermed foretatt N * N = N² sammenligninger, også kjent som kvadratisk kjøretid.
I det verste tilfellet er N = 50 000, som gir 2 500 000 000 sammenligninger, altså 2,5 milliarder.
Ved å lese på siden om kjøretid, ser vi at maskinen nødig klarer mer enn 100 millioner operasjoner per sekund, og det må isåfall være svært enkle operasjoner, og ikke i et språk som Python.
La oss se om algoritmen heller kan designes på nytt, for å redusere antall operasjoner.
Algoritmen - forsøk 2
Det finnes mange måter å unngå kvadratisk kjøretid.
Dersom vi bruker en dict() for å telle om hvert element er sett én eller flere ganger,
vil hver operasjon i dict-en være uavhengig av størrelsen på dict-en.
Dermed vil den totale algorimen få en lineær kjøretid, siden den gjør N operasjoner.
En annen mulighet er å sortere listen, med liste.sort().
Når listen sorteres, vil alle duplikater av samme tall ligge inntil hverandre, som gjør det lett å sjekke om et tall faktisk er unikt. Så lenge begge nabo-tallene er ulike, er tallet unikt, og siden vi kun bryr oss om det laveste unike tallet, kan vi begynne med det laveste tallet, og stoppe så snart vi ser et unikt tall.
Sortering er en mye brukt teknikk som er innebygd i alle språkene, og som kjører i O(N log N),
en kjøretid som bare så vidt er dårligere enn lineær kjøretid.
Under følger to forslag til løsninger. Begge gir 100 poeng på oppgaven.
dict-basert løsning
N = int(input())
liste = []
for i in range(N):
tall = int(input())
liste.append(tall)
# Tall som er sett én gang har unikt[tall] = True
# mens tall som er sett flere ganger har unikt[tall] = False
unikt = dict()
for tall in liste:
if tall in unikt:
unikt[tall] = False
else:
unikt[tall] = True
# Lag en liste med kun de tallene der unikt[tall]=True
unike_tall = [tall for tall, unik in unikt.items() if unik]
# print laveste unike tall som sist, eller -1 om ingen tall er unike
if len(unike_tall) == 0:
print(-1)
else:
print(min(unike_tall))
sort-basert løsning
N = int(input())
liste = []
for i in range(N):
tall = int(input())
liste.append(tall)
# sort putter de laveste tallene først
liste.sort()
for i in range(N):
# Dersom vi har et nabo-tall til høyre og/eller venstre,
# og noen av naboene er like oss selv, så er dette tallet ikke unikt
if i > 0 and liste[i-1] == liste[i]:
continue
if i+1 < N and liste[i+1] == liste[i]:
continue
# Hvis ingen av naboene var like, printer vi dette tallet og stanser programmet
print(liste[i])
exit(0)
# For-løkken fant aldri et unikt tall, print -1
print(-1)